Neural Networks: Mathematics and Interpretation
My aim in this blog is to give some behind the scene/mathematical introduction to the neural networks.
I believe that it is needed in order to build a good neural net model and to have reasonable expectations from it.
Neuron/Perceptron
What is it?
A: Just a simple equation
y=f(∑(xᵢ × Wᵢ)+b₀)where,
- y is the prediction
- f is a non-linear function
- xᵢ is the datapoint/input
- Wᵢ is the weight, which will be learned
- b₀ is a bias
Another way of representing

(Source: https://docs.opencv.org/2.4.8/_images/neuron_model.png)
Why is this math required?
We aim to find a combination of inputs and a transformation to help us predict.
For example, consider a classification problem:

(Source: https://www.researchgate.net/profile/Katarzyna_Marzec/publication/259821431/figure/fig3/AS:296973505712135@1447815409944/General-scheme-of-a-classification-problem.png)
Why is the use of bias?
A line without bias:
y=mxi.e. a line passing through the origin
(Source: Wikimedia, https://upload.wikimedia.org/wikipedia/commons/0/06/Intercept_Form_Example2.PNG)
A line without bias:
y=mx+c(Source: Wikimedia, https://upload.wikimedia.org/wikipedia/commons/7/7d/Intercept_Form_Example1.PNG)
So it will help your classifier move
How does f (non-linearity) help?


Most used activations:
- Linear:
y=f(x)=x
- Sigmoid, Tanh, ReLU
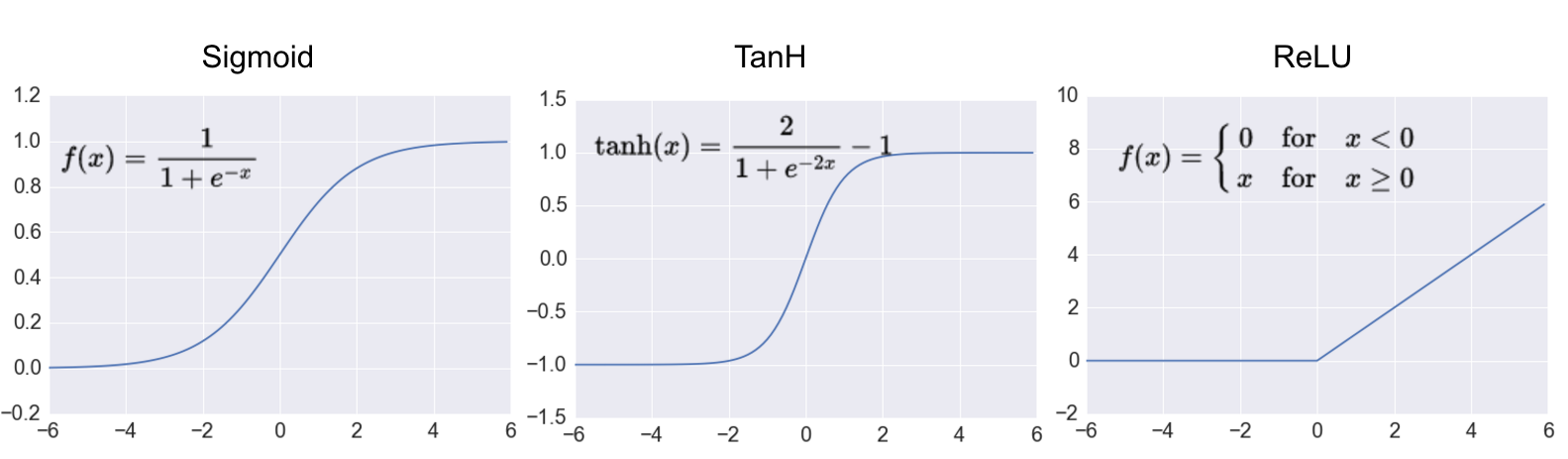
(Source: mc.ai blog on deep learning)
- Hard-Sigmoid:
y=f(x)=max(0,min(1,x×0.2+0.5))It is an approximation of the sigmoid. This activation is the default activation for RNNs in Keras for increasing speed.
How is it done?
Ans: Matrix Algebra
A look back:

(Source: Peter Krumins’ blog on Matrix Multiplication)
Check the relation between output and input dimensions:
(row×midcol)∗(midcol×col)=row×col
(Source: Peter Krumins’ blog on Matrix Multiplication)

Check the dimensions:
(1×n)∗(n×1)=1×1(1×n)∗(n×1)=1×1Matrix Notation:
Y=WX+bIf we apply a non-linear function:
Sigmoid: Y=σ(WX+b)
Tanh: Y=tanh(WX+b)
MLP: Multi-Layer Perceptron
Multiple neurons together

(Source: Wikipedia page on Artificial Neural Nets)
How to do it with a matrix?

Check the dimensions:
(1 × n) * ( n × h ) = (1 × h )
h is the hidden layer size
A different way

Looks neat right? what about hidden layers

What if I take multiple columns together?
That’s what we usually do

b is called the Batch_Size
Same Matrix notation everywhere:
Y=f(WX+b)So each hidden layer is a classifier in its own. We are putting up multiple classifiers together
A popular example
XOR Gate:

(Source: http://www.saedsayad.com/)
MLP:

(Source: Victor Lavrenko’s YouTube tutorial on Neural Nets)
Try out Google Playground
BTS
Each of the neurons is mathematically a linear plane with some non-linear transformation. The plane exists in an n-dimensional space where the features are the constituting dimensions.
Effectively, each neuron is a classifier (and a feature generator). A neural network has multiple of such neuron which acts as the input to another neuron. Take the neural net for XOR from the example above: You see two classifiers (yellow line and blue line). The next neural net uses the boundaries defined by them to make the inference.
Let’s see how does the non-linearities get combined together in a neural net.
I am taking an XOR-like input on the playground and will use ReLU as the activation. Consider the following two cases:
Case 1:

Case 1 shows the examples of our conclusion that ‘each neuron is a classifier’. The data requires only two classifiers and that’s how the model is working in Case 1. The classification boundary is also shown for each neuron.
You may say that a neural net is a combination of multiple classifiers.
Case 2:

Case 2 shows what happens when our model is more complex than required. It wouldn’t affect the performance. But it will also have lots of redundancy. The dashed lines represent the weight strength in the playground. Now check following:
Hidden Layer 1 (4 neurons):
- 1st and 2nd neurons are essentially the same as inputs
- 3rd and 4th neuron are same
Hidden Layer 2 (3 neurons):
- 3rd neuron is more important than other in classification (output weights are stronger)
- 3rd neuron mostly depends on those neurons which are similar to the input
Before we make conclusions about the effectiveness of one over another, here is a confession: I had to manually set weights in Case 1. It was not reaching the same conclusion after multiple trial-and-error.
What about the input data itself? What kind of value does it add?
Here are two cases for it:
Case 3:

v/s
Case 4:

As you can see, if you have the relevant features available to you, your network will be able to classify better.
I believe many would disagree with me on this. In fact, a big reason for industry to move towards deep learning is that it performs the feature extraction for you. That is also my point; if you already know what input is good, use it to make the model learn faster.
One last point: many people assume that the number of neurons should always decrease in subsequent layers. I would leave it for the reader’s consideration with the following:

